Formative assessment does not improve learning

Education in the UK is susceptible to passing fads and fashions, which often results in a knee-jerk reaction from those headteachers who fall into the trap of believing it is important to have in place every new shiny bell and whistle before an inspector rocks up at the gates. The truth of managing a school well is quite different; it is not the job of a headteacher to impose a never-ending cycle of initiatives, rather being a headteacher is about being the intelligent, humble custodian of an educational institution for a period of time. Doing the job well means being well informed, careful, and strategic. Our knowledge of how learning occurs continues to increase and mature – headteachers should, of course, be cognisant of this new knowledge and should plan to bring those advantages to their pupils in a well thought through approach with the support of their well-trained staff. This is a far cry from forcing intelligent teachers to implement unproven fads and fashions at the drop of a hat.

A major problem arising from the UK’s tendency to take the scattergun, shiny new toy approach is the meaning of highly effective approaches, with firm findings from research to support them, is lost or misconstrued. Instead of careful integration of new educational knowledge, all too often we see well defined and well-designed pedagogical improvements being reduced to meaningless, mind-numbing initiatives.

Take, for example, the knowledge discovered and refined over many decades by educators, cognitive scientists and psychologists, there is clear benefit to pupils when they are asked to recall previous ideas and this benefit is even present when pupils are forced to retrieve memories simply by encountering questions without the need to answer them correctly – a ‘testing effect’ arises, where learning is improved as pupils necessarily have to re-member, which is to say they must create a new memory. It is an interesting finding and is reliably replicable in the laboratory and in the classroom. Headteachers and teachers should be aware of these benefits and plan for occasions when pupils will be required to retrieve prior knowledge. There is much more to it, of course – the literature on ‘testing effect’, ‘retrieval practice’, ‘spaced learning’, ‘method selection’ and myriad other intriguing consequences of recalling earlier learning is extensive and goes back many decades. Teachers have known about these effects for a very long time indeed and, for many expert teachers, it is an embedded stratagem in their repertoire of pedagogic choices. All well and good. But then…

Well, then along comes a fresh packaging of these old ideas and a PR campaign to promote them. However, contained within the fresh, shiny new packaging is not a detailed, nuanced, complex exploration of a profound idea, but a significantly diminished version – one designed to fit with today’s need for pithy explanations and easy implementation. In our example, the result is a diktat handed down by the headteacher, who does not wish to engage with the literature and is content with a pithy summary, demanding all teachers must now bolt on to the beginning of every lesson a 10 minute ‘retrieval practice starter activity’. And so, once again, the profound becomes the mundane, the impactful becomes the time sink, the years of research and development becomes the easy to roll out initiative. Box ticked, inspector happy. Or so the unthinking headteacher smugly assumes.

There is, of course, nothing new about this problem. The dumbing down of educational discourse has mirrored the very same dumbing down in all public debate since the mid 1990s. Though, given education should be in the very business of defending knowledge and truth, it is particularly saddening schools have given in to the modern pressure to do away with nuance and conviction to be replaced with anodyne, simplistic consensus.

I recall attending a training day in the late 90s at which a colleague I had hitherto regarded as smart and diligent presented a session on Paul Black and Dylan William’s rather excellent assessment summary, ‘Inside the Black Box – Raising Standards through Classroom Assessment’, which I had already read with interest. My colleague rushed through a few slides and ended with an instruction to all teachers their lessons must now contain ‘formative assessment’ because ‘formative assessment improves learning’. This was curious for two reasons. Firstly, how odd it was to assume any teacher sitting in the hall that day did not already frequently use formative assessment approaches as a normal part of their teaching. Secondly, it is incorrect.

After about the fifth or sixth time of my colleague saying the line, ‘formative assessment improves learning’, I raised my hand to ask to speak. A groan from those teachers who just wanted all of this to end. And then I said, ‘it simply isn’t true to say formative assessment improves learning. It does not. It is the actions one takes based upon this formative assessment which might possibly improve learning’.

I didn’t think this a controversial thing to point out, but his presentation contained absolutely no discussion of what pedagogic actions teachers could take based on different outcomes from the formative assessment activities he was promoting (which, by the way, appeared to be colouring in pupils’ names in either red, amber or green on a spreadsheet for no discernible reason).

So, there are two outcomes from the recent trend to dumb everything down; really bad ideas make it into the classroom and cause teacher burnout from initiative overload, and really good ideas are so diminished they become easy to dismiss or to demonise by those who do not act in good faith.

By way of example, consider the debate around Deliberate Practice. Deliberate Practice is a long-established approach which, although variation exists in its implementation depending on circumstances, has a set of core elements defining its use. It has its proponents and opponents. And, because so many people refuse to properly engage with the literature, it has been easy for its opponents to claim Deliberate Practice ineffective and, therefore, to steer teachers away from its use. Perhaps the most egregious example of this was the 2014 meta-analysis by Macnamara et al. This study set out to diminish the importance of Deliberate Practice and concluded it ‘not as important as has been argued’. Many people quickly pulled together pithy reports (or even Tweets) to announce the nail in the coffin for deliberate practice. Yet few (perhaps none) bothered to read and stress-test the report. In fact, Macnamara et al made this claim even though their own report found an effect size of 0.38 for the influence Deliberate Practice has on performance. You may well ask, is an effect size of 0.38 worth changing policy over? Well, to put that figure in a more everyday context, here are the effect sizes some certain behaviours have on mortality: obesity (0.08), excessive alcohol consumption (0.13) and smoking (0.21). These are much lower, but we all agree are not to be ignored (indeed, consider how much public money is spent trying to change these behaviours and you’ll have a good sense of how important society thinks these effect sizes are).

So Macnamara et al find a significant effect size and yet the wording of the report is used by many to claim Deliberate Practice is not important. That’s odd. But nowhere near as odd as the truth.

Of the 88 studies Macnamara et al used in their meta-analysis, 18 were not even about Deliberate Practice. This enabled the reporters to manufacture a lower effect size. When those 18 studies (which contribute 45 effect sizes) are removed from the calculation, the effect size for Deliberate Practice increases further still. Why include 45 effect sizes in a report about Deliberate Practice when those effect sizes are completely unrelated to Deliberate Practice? Could it be because those who wish to oppose (or support) a specific approach (perhaps because of their own ideological beliefs) know the teaching profession has succumbed to the soundbite? Thankfully, we have the likes of SD Miller et al who are not willing to simply accept a pithy line – this group re-examined Macnamara et al (2014) in their 2020 paper ‘To be or not to be (an expert)’ and highlighted the flaws in its methodology.

So, should teachers take time to plan for Deliberate Practice and formative assessment and a whole host of other approaches painstakingly evaluated for efficacy over decades? Yes. But…

As I said to my colleague all those years ago, formative assessment does not improve learning, it is the actions one takes based upon the formative assessment that count.

Learning is complex. There is not a single method to be deployed and all will be well. Rather, it is about the combining of tactics and choices, in real time, with real teachers and real pupils in a responsive dialogue with each other. Deliberate Practice does have a good impact on performance, but it’s just one of many ways of increasing the chances of successfully bringing about long-term, durable learning.

We should, therefore, deploy as many of these proven approaches as we can as pupils ascend from novice to expert with any new idea. There is a cumulative effect. In much the same way taking steps to avoid obesity (ES = 0.08) does not really shift the needle in terms of how long one is likely to live, combined with avoiding excessive alcohol consumption (0.13) and smoking (0.21) and other known impactful behaviours, the cumulative effect really starts to make all the difference. As a pupil moves from a novice appreciation of a new idea, teachers can draw on proven methods of checking and securing prerequisite knowledge, bringing about awareness of new knowledge by making connections, moving the knowledge from an initially inflexible state to a flexible one, such that motivation to push ahead can be achieved and teacher and pupil can continue the dialogue in a responsive cycle of teaching and learning until the pupil gains an automaticity with the new idea and can use this success to move through naive, purposeful and finally deliberate practice, which, in turn, gives the pupil such secure foundations and a fluency of understanding that they might make wider connections in knowledge and behave as a domain expert might behave to achieve a mature appreciation of the new idea. Moving through these phases of learning, the teacher deploys numerous proven tactics, each with their own effect. Standing alone, these individual effect sizes may well be small, but combined the overall impact is great.

In my 2019 book, Teaching for Mastery, I described the journey through these phases of learning in a single diagram of the mastery cycle and emphasised the importance of not breaking the cycle. The elements are of little utility when used in isolation – the power comes from combining them in an expert teacher repertoire. Do not allow a consultant to tell you things like ‘formative assessment improves learning’ without insisting the conversation goes further to explain all educational interventions, such as formative assessment, are but one part of a whole.

Differentiation

During a recent visit to a school, a head of mathematics explained the school's vision of differentiation as simply pupils ending up with different outcomes - some pupils, for example, would complete the red exercise of problems, some the amber, some the green.  The problems in one set were, in the classrooms visited, unrelated to the problems in another.  I asked the HoD, 'so, differentiation is basically the view some pupils can learn the stuff you wanted them to learn and others can't?'

I think 'differentiation by outcome' is a dreadful, reductive view of education.  A view that promotes the entirely wrong idea some pupils can learn well and others pupils cannot.

Instead, I view differentiation as the set of actions a teacher takes in order to guarantee all pupils learn well.

It is a big topic to do justice in a very short blog, but here's a quick stab at describing a more useful view of differentiation...

If we are working with more than one pupil, then it is always the case there will be variation in the experiences the pupils have had to date, in their understanding of ideas, in the maturity of their knowledge schemata, in how quickly they can make sense of a new idea, and in how keen they are to do so.

Differentiation is simply a teacher’s response to all of the variations existing within a class. Understanding the class is made up of individual human beings with unique and different lives means teachers can appreciate the burden upon them to ensure all pupils have a successful experience of learning whatever new idea the teacher is planning for them to understand.

So, differentiation is just a way of saying how the teacher reacts to the pupils in front of them. This is a continual process and changes from class to class, idea to idea, even day to day. Perhaps it is helpful to consider the phases a teacher and class progress through as they work together on a new idea.

To begin with, the teacher will seek to establish the pupils’ ‘readiness’ for learning a new idea – this could be through some sort of diagnostic activity or through discussion or through detailed prior knowledge of the pupils. Clearly, pupils will have differing levels of readiness – some will have forgotten things, some will have missed key moments, some will have independently prepared more than others, etc. The first stage in differentiation, then, is the actions the teacher takes based on an individual pupil’s readiness. For some pupils, the teacher may react by providing corrective instruction, working carefully to undo and overcome a misconception, for example. For other pupils, perhaps some pre-teaching will help them to connect partially forgotten ideas. Other pupils will be perfectly well equipped to proceed with new learning having demonstrated their readiness by mastery of the diagnostic activity – the teacher might react here by extending the pupil’s domain expertise in a prerequisite idea by asking them to work on an unfamiliar problem or they might simply allow the pupil to progress to the new learning. This will depend on the teacher’s plan for classroom management and whether or not they wish all pupils to receive the introduction to the new idea together.

When pupils are ready to learn a new idea, the next step is instruction. We know understanding new ideas relies on understanding earlier, pre-requisite ideas. This is how we construct new knowledge – by linking it to what is already understood and using this understanding to ‘bridge’ to new meaning. The teacher can do this by using story-telling and metaphor. To enable metaphors to come to life and have mathematical meaning, the teacher uses models. The models are explored in examples and these examples form the way of narrating the instruction.

The second step in differentiation is, therefore, when teachers react to how readily (or not) pupils are making sense of the instruction. They do this by changing the examples, the models and the metaphors they are using to animate their instruction. The order in which these changes are made is really important. I have previously written about how to react during the instruction phase in this blog, Models, Metaphors, Examples and Instruction

All pupils (all people, in fact), grip new ideas at different speeds. The purpose of instructing pupils is to bridge from a mathematical idea in my head and understood by me to one that the pupil is able to make meaning of. Working out whether or not the individual pupils in front of us are making appropriate meaning is best achieved through dialogue – as we narrate an example, we then ask them to work on a similar problem and narrate back at us their thinking. In other words, we are using the to-and-fro of examples and problems as a conversation between teacher and pupil – the pupil is forced to articulate their meaning.

The next step in differentiation is, therefore, to react to the pupils in front of us by varying the number of examples they are asked to respond to until each individual is communicating the meaning the teacher is aiming for. This is just a way of checking that the meaning is being received. We should not be fooled into thinking their ability to articulate the correct meaning is an indication that any learning has taken place. At this stage, it hasn’t. But we do now know that we are able to ask the pupils to work independently on problems. We can now ask them to do some mathematics.

Doing mathematics is an absolutely vital step in learning mathematics – it is through doing mathematics pupils begin to truly learn mathematics.

It is important we do not stop at the point of them simply knowing – the point they were able to give the correct articulation. Imagine a pupil learning to play piano, for example. The teacher could tell them the keys they need to press and the order in which they must be pressed, with what pressure and at what pace so as to produce a certain tune. And the pupil could articulate back at the teacher the precise instruction – they know how to play the tune. But that doesn’t mean they can play the tune.

A teacher could explain, through the use of several examples and problems, how to multiply over a bracket, say, and a pupil might articulate back at the teacher the precise instructions – they know how to do it. But that does not mean they can multiply over a bracket. This is why we now give the pupils ample opportunity to actually do the mathematics. We want pupils to be so competent in doing the new mathematics they achieve a fluency in doing so. That is to say, they can perform precisely without the need to give attention.

The next step in differentiation is clearly the amount of doing we ask of individual pupils – they will all achieve fluency at different rates.  Initially, this doing might be thought of as naive practice. Once the new skill is something pupils are comfortable with, it is time to start learning.

This might sound a trifle odd and some people will argue, surely, if the pupils are fluent, they have learnt what they need to. But this is just the first step. Learning only occurs at the boundary of our current ability. All pupils have pretty much unlimited potential, but they only continue towards expertise if they continue to operate at their limits. Automaticity is a poor aim for any lesson – it represents a pupil who is no longer learning.

To ensure learning is becomes long term and durable, we now ask the pupils to engage in practice.

Effective practice occurs in phases too. Firstly, teachers should create opportunities both in the classroom and beyond, for pupils to engage in purposeful practice – this type of practice is goal driven. Considering the mathematical skill the pupil has been working on and now has automaticity with, teacher and pupil examine carefully the common errors the pupil is making.

For instance, the pupil who can fluently multiply over a bracket may well forget to multiply the second term in the bracket two times in every, say, ten questions. We now have a goal – it is highly specific to the pupil and, through dialogue with the teacher, the pupil can set about undertaking more practice with an awareness of that goal – they can be looking out for the common mistake they make and can try to reduce the number of times they falter to, say, just two times in every forty questions. Purposeful practice can be carried out independently at home because the pupil has a success metric to give them continual feedback and spur them on.

Purposeful practice keeps the pupil at the limit of their competence and, therefore, creates the cognitive conditions for learning to occur. So, the next step in differentiation is how the teacher reacts to the pupil’s need for purposeful practice – varying the amount of practice, the goals and the feedback to best realise the individual pupil’s limitless potential to learn. A pupil can significantly improve their mathematical skill through purposeful practice. But it does have its limitations, since purposeful practice leaves the pupil to determine how best to overcome their common mistakes.

The next stage in differentiation is, therefore, how the teacher responds to the pupil’s progress with their personal purposeful practice by deciding what type of deliberate practice to provide to the individual pupil. Deliberate practice is also goal driven, but draws upon what is already known in a domain to improve performance. With the pupil above, who has been forgetting to multiply the second term, the teacher can coach them in overcoming the problem by telling them about tried and tested ways for doing so. In other words, in the deliberate practice phase, the teacher trains the pupil in the approaches that experts in the domain have developed and used to overcome the very specific problem they are facing.

The final stage of practice is designed to help further assimilate the new learning with the pupil’s developing schema of knowledge. Now, practice problems are randomly mixed with problems of earlier learnt ideas – this removes recency and cue from the pupil’s practice exercise and forces them to retrieve previously learnt skills and to identify when to select certain mathematical tools.

The final stage in differentiation is, therefore, the teacher’s reaction to a pupil’s agility in selecting appropriate methods in mixed problems – all pupils will improve their method selection at different rates, so the teacher carefully judges the amount of practice required and supports the individual pupil as required.

This view of differentiation can be thought of as the oft quoted idea of learning being like building an enormous edifice. Constructing a mighty building requires very careful placement and gradual levels of scaffolding. Here, the teacher is the scaffold, providing all the necessary support and rigour needed for the pupil to fulfil their potential.

And just like the construction of an edifice, it is key that the scaffolding is removed at the right moment to let the building shine.

Limitless - Part 2

Stages of Learning

 

In Part 1 of this blog, I set out an argument that not all stages of learning are the same and that these different stages have different characteristics.  It is by understanding this and understanding the specific requirements placed on teachers at each stage that enables us to work with pupils in such a way that every single pupil is able to learn well and attain expertise in a subject.

 

I urge teachers and all involved in education to reject those assertions made about learning, based on examining just one single stage of learning, which attempt to portray teaching approaches as black and white, as good and bad.  Most often, when we dig into all the bold claims being made as a retort against someone else’s bold claim, we find that each side has a point.

 

By stepping back and considering learning from a distance, we can see that it is a complex process; one that sees a pupil arrive novice and leave expert, through a long and necessary period of maturation.

 

In this part of the blog, I will discuss learning as a continuum of stages.  The reader should not take the presentation of these stages to mean that they are distinct or indeed that they are linear – learning can be undone as readily as it can be built, so there is always likely to be a toing and froing between these stages.  Also, the reader should not conclude that I am suggesting these stages as a full and final description of learning.  I use these stages simply to give structure to the conversation.

 

We know a heck of a lot about learning.  Approaching teaching armed with humanity’s cumulative knowledge about teaching means we can be forensic rather than random, we can be sustained rather than faddy, and we can be unswerving in our belief that all pupils can learn well.  I think that’s no bad thing.

 

I think we can consider the stages in learning as being grouped into two broad phases, namely

 

1.     Short-term knowledge acquisition phase

2.     Durable knowledge growth phase

 

(Sidenote: I use the phrase short-term here deliberately, because I wish to highlight certain common aspects of classroom practice.  But I am, of course, aware that I don’t really mean short-term; when knowledge is properly acquired, it doesn’t really leave us.  It may well be out of reach and it may well seem long forgotten, but it is more often the case echoes remain, somewhere unknown and somewhere not yet understood.  As a way of illustrating this point, try to think, for example, of a phone number or address or the layout of some streets from many years ago.  They seem lost.  But, if you were to be shown, let’s say, a list of four different phone numbers and asked to state which one of them was your childhood number, you will pretty much always get this correct.  There’s an odd sensation when this happens – it feels rather good – and suddenly some other memories come back to life too.  What is happening at this moment is a process of re-membering; your brain is creating a brand new memory associated to the fact at hand.  This process of re-membering has a significant impact on the ability to recall later; the more times you recreate memories about a fact, the more readily you will be able to bring it to mind again.

 

For more discussion on cognitive architecture and memory, see my 2019 book, Teaching for Mastery.)

 

I present these two broad phases and the stages comprising them in a simple graphic, which I find helps in discussing the idea.  I would not wish anyone to assume that this image is indicating a strict hierarchy, though, so please take with a huge pinch of salt.

 

 

These stages can be considered personal qualities that the pupil acquires as they make progress in learning.  Each can be broken down further into stage-specific actions / dispositions / techniques as summarised below.

 

Awareness

·      Readiness

·      Story

·      Metaphor

·      Model

 

Inflexibility

·      Exposition

·      Example

 

Flexibility

·      Non-example

·      Boundaries

·      Variation

·      Principles

·      Structures

 

Automaticity

·      Replicate

·      Rehearse

·      Practise naively

 

Fluency

·      Practise purposefully

·      Practise deliberately

 

Connectivity

·      Forward facing

·      Transfer

·      Method selection

 

Maturity

·      Embed and behave

·      Understand the Battleground

·      Assimilate future learning

 

 

What follows is a brief description of how we might bring about those qualities.  In Part 3 of this blog, I will consider each stage more fully, illustrating what these might look like in the classroom.

 

Bringing about Awareness

 

At the very moment of encountering an entirely new idea, all human beings rely on the same mechanism for successful learning; extending what we already know and believe to be true to make sense of a novel situation.  We make sense of a new idea – literally being able to make new memories and new meaning – by translating the unknown into the known.  We can accept new ideas if they make logical sense in the framework of what we already know and understand.

 

When describing a new concept to pupils, teachers must engage in a dialogue – we cannot simply pour new knowledge into the minds of pupils, we must negotiate the new meaning into existence in the pupil’s mind.  Teachers use story to achieve this.  They draw on metaphors, models and examples to weave together a story that pupils can make sense of because they have the underpinning grammar available to them that allows them to understand the narrative, they link the models and examples to ideas they already firmly understand, and they make logical, believable steps to convince themselves of the new truth.

 

This is only possible if the new idea can be translated into known ideas and this is only possible if the new idea is not too far beyond the pupil’s current understanding.  We want pupils to grip every new idea they encounter; this starts with becoming aware of the idea in a meaningful way.  This can only happen when the prerequisite ideas – the ideas that allow us to have the discussion about the new idea – are secure and brought to mind through story.

 

All of this is a rather longwinded way of saying that, before we embark on teaching a pupil a new idea, we must determine their readiness.  There is no point in trying to teach anyone an idea so far beyond their concept of reality that they are bewildered and left feeling as though everything is being discussed in an alien language.  If a pupil does not have a secure grip of the necessary prerequisite ideas, teachers should step back and address that issue before attempting to bring about new meaning.

 

Bringing about awareness of a new idea is a disruptive process – in a very real sense, we are asking an individual to change their view of the universe – but it need not be a difficult process, since we are able to bridge from the pupil’s current knowledge in small, logical leaps.

For more on bringing about awareness, see my 2020 blog, Models, Metaphors, Examples and Instruction. 

 

Bringing about Inflexibility

 

When a pupil is aware of a new idea and it has begun to permeate their mind, sparking off connections to previously understood ideas, we can move further with the idea to a point where the pupil can gain a limited appreciation of how the new idea might be useful or might react or might inform or might be deployable.  Teachers can achieve this further insight through exposition and example.  We are not attempting here to bring about a durable understanding of an idea and all its implications, but merely setting out to give the pupil a foundation of success and comprehension that they may continue to build upon.  Early success in gripping some of the applications or surprises or joy or power of a new idea can play a key role in creating conditions in which pupil ‘grit’ will sustain them through further study of the idea.  These early steps in working with a new idea can be as simple as seeing that the new idea is a time-saving device for a simpler but long-winded approach with which the pupil is already familiar – recall, for example, learning a new formula in a spreadsheet and realising you no longer must do tedious data entry.  That feels good, right?  A teacher has told you how to use a formula, you can use it, it has benefit, it brings about a sense of pride and success and maybe sparks an interest in learning more about these types of approaches and maybe enables you to start that learning with a sense that, although you’re not quite sure why everything works, it will be something that will be worthwhile and will be surmountable.

 

Inflexible knowledge is limited.  We are using new ideas in a restricted set of circumstances, and we are doing this deliberately.  Attempting to appreciate the full range of meaning with a new idea is not a good strategy – we can all learn well, but only when we’re learning at the boundaries of our current understanding, which is not usually possible if we try to take in all the implications of a new idea at once.

 

The teacher can use exposition to carefully and explicitly, with detail and with specific examples, instruct the pupil.  We tell them the facts; we tell them what to do.

 

I will pause here for a moment to put to bed any silly notion that inflexible knowledge is a synonym for ‘rote learning’.  Rote learning is a term thrown around by those who wish to paint an entirely false picture of what teachers do.  Rote learning is remembering facts in the absence of meaning.  Almost no learning is rote.  And it is vanishingly rare to see any teacher instructing without meaning.  Using the slur of ‘rote learning’ as a way of discouraging teachers to take the crucial step of first establishing inflexible knowledge is simply an attempt to prevent all pupils from learning well.  Inflexibility is knowing, remembering, and using facts with meaning but within deliberate constraints that enable pupils to experience early success and motivation.

 

When using examples to bring about inflexibility, teachers should vary the examples they use in their discussions and limit the number of problems pupils work on.  We are in the short-term knowledge acquisition phase and the nature of practice is fundamentally different in this phase compared to the later durable knowledge growth phase.

 

Bringing about flexibility

 

Inflexible knowledge is a great motivation generator, but we would never wish to leave pupils limited.  By examining examples and non-examples, teachers and pupils can iterate towards a set of circumstances when the new idea holds true and when it does not.  Pupils can identify the boundaries of the new idea and have a much greater appreciation of when it is appropriate to apply the idea or not.

 

Bringing about flexibility means to bring about an understanding of how, when and why an idea is useful and appropriate.  Teachers can guide pupils through carefully sequenced activities, deliberately varying the conditions such that pupils discern the underlying principles at play and get to view the mathematical structure supporting the idea and its applications.

 

Bringing about automaticity

 

Once a pupil is familiar with an idea, some of its applications and some of its limitations, we seek to empower the pupil by bringing about automaticity in working with the new idea.  In other words, we set up activities and obstacles that they work through until they are able to perform without taking up great amounts of mental energy.

 

Teachers can work through detailed examples, applying the new idea in useful ways, narrating in detail the how and why of each step in the example, highlighting key moments and features and role-playing that sense of achievement when an apparently intractable problem is overcome.  In return, pupils work on their own problem, replicating the steps the teacher has taken and paying careful attention to the key moments.  This batting to and fro between example and problem, is a technique teachers use to ensure pupils have received the meaning they intended and can articulate the approach for themselves.  When both teacher and pupil are confident they are singing from the same hymn sheet, the pupil can then engage in rehearsal; working with the new idea without the support of the teacher.  This rehearsal does not require the pupil to work through endless questions, since here we are simply checking that meaning has been received rather than attempting to refine a pupil’s accuracy.  At this stage, working on a small number of problems, but giving great attention to each, articulating to others (teacher or peer), and carefully unpacking the meaning of every step or decision, is far more important than simply getting through a list of questions.

 

Pupils can then progress to what we might call naïve practise, which sees the pupil working on problems with a general sense of what they wish to achieve and attaining a level of performance that is more or less automatic.

 

Recently, particularly in England but also in other Western systems, automaticity has become the goal of teaching and learning.  This is a really bad goal.  Automaticity is an important stage in learning, but hitting this plateau of performance means that pupils remain in their comfort zone and do not progress to expertise.  Naïve practise resulting in automaticity is the kind of practice that most of us undertake in most areas of life; we achieve a point of ‘good enough’.  We are in our comfort zone, don’t feel like a fool, are able to perform in most day-to-day situations and can feel good about what we are doing.  For most of us, in most domains, ‘good enough’ is, well, good enough.  But what we wish to achieve as the teacher is to reveal to pupils the awe and wonder of being expert.  Ascending to elite performance necessarily requires us to operate at the limits of our comfort zone continually and not to be seduced by ‘good enough’.

 

Being at the limits of one’s comfort zone can be unpleasant – it can feel exhausting or frustrating or just damn right hard.  To be able to persevere through difficulty requires ‘grit’.

 

All of us have some domain in which we willingly persevere in the face of difficulty (it is not yet known why this is the case, but there are some interesting studies indicating a genetic link to predisposition for perseverance in given circumstances).  This ‘grit’ appears to be domain (subject) specific, which means schooling might be thought of as a race to discover the domain(s) in which a pupil will willingly persevere through tedium, pain, exclusion or sacrifice.  It is vital that we do make this discovery for every single pupil or else their experience of schooling is one in which they never feel the wonder of expertise.

 

This puts an end to the stupid idea that there are pupils who can learn well and pupils who cannot.  All pupils can.  But they will have different levels of grit in different subject areas.  Teachers already know this and have known this for a long time.  We all know the pupil who is switched off in the mathematics classroom but on fire in the history classroom, for instance.

 

The trouble with the ‘grit’ debate is that it is sometimes used to excuse pupils from effort in those domains they do not have a proclivity towards.  This is fair enough when we reach the highest levels of a domain, but for school level learning, it is possible to bring about in pupils a level of grit necessary to take their deftness with school level ideas to, or close to, expertise.  We can think of this level of grit as ‘flow’.

 

Flow is a state of concentration, low self-awareness and enjoyment that typically occurs during activities that are challenging but matched in difficulty to the person’s level of understanding.

 

It is interesting to note that there is:

 

·      Negative correlation between flow proneness and neuroticism

·      Positive correlation between flow proneness and conscientiousness

·      No correlation between flow proneness and intelligence.

 

Which is to say, flow proneness is associated with personality rather than intelligence.  This is another nail in the coffin of the entirely wrong notion that only intelligent people can apply themselves with determination.  It is important to keep banging this drum; all pupils can learn well.

 

I will cover the concepts of ‘grit’ and ‘flow’ in depth later, but for now it is useful to consider ‘flow’ as a state of effortless attention that relies on different mechanisms from those involved in attention during mental effort.

 

With forensic teaching and an appropriate level of pupil grit, the ascent to expertise can continue for all.

 

Bringing about Fluency

 

Fluency is a state in which a pupil no longer finds it necessary to attend in order to perform with skill.

 

This state has a key difference to automaticity, when the pupil could perform without the need for great attention and understood what they were doing.  That difference is skill.

 

‘Skill’ can be summarised as ‘reliably replicable knowledge’.  The emphasis here is on the ‘reliably’.  So far, the type of practice that the pupil has engaged with has been aimed at attaining an effortless ability to do. By understanding the idea, knowing about its underlying principles and its boundaries, knowing when it is appropriate to apply the idea, and having rehearsed the idea to a level of comfortable familiarity, the pupil is able to articulate their understanding and solve problems using well embedded procedures.  But, like all of us who have practised anything to the point of ‘good enough’, the pupil will regularly make errors – these are genuine slip ups, not an indication of a lack of understanding, but just natural inaccuracies in following an algorithm, procedure or approach.

 

Our ambition now for the pupil is for them to become skilled at working with the idea.  This means they will be able to replicate an appropriate application of the idea reliably – their performance becomes elite rather than just good enough.

 

Naïve practise will not achieve this.  The pupil must be made aware of their level of accuracy and the micro ideas or steps contributing to working with an idea that are cropping up as natural errors from time to time.  This could be through feedback from the teacher or a whole host of instant feedback methods (such as being shown worked solutions or having a digital programme monitor steps and pinpoint advice).  The critical point is that the feedback is timely – that the feedback happens in real time.

 

Armed with the knowledge of the slips they are making, pupils can now engage in a more powerful form of practise, which is most often referred to as ‘purposeful practise’.  Purposeful practise, as the name suggests, has a purpose; the pupil has an aim to improve their accuracy.

 

How accurate should the pupil become?  How much practice is required?

 

The answer to these questions will vary depending on the importance of the idea and how much future learning rests upon it.

 

Suppose a pupil wishes to secure their knowledge of multiplication facts through to 10x10.  Are you ok with them getting one in every 10 questions incorrect?  One in every 30?  Or 50?  Or 100?  What if, instead, it was a heart surgeon performing an operation?  What level of accuracy might you be comfortable with then?

 

These incremental improvements in accuracy for the pupil act as targets.  The pupil who is making one mistake in 10 problems can be given the target to reduce their error rate to one in 20, say.  And so on.  The pupil can work with purpose because they have immediate feedback and a concrete goal to achieve. 

 

Purposeful practise can significantly improve a pupil’s accuracy and take them much closer to true fluency, but to really nail this stage and acquire the quality of fluency, we have a final tool at our disposal; deliberate practise.

 

Deliberate practise brings into play the most powerful weapon a pupil has in their fight to learn more and more and more: the expert teacher.

 

Rather than the pupil simply working hard to improve their accuracy based on the binary feedback of correct or incorrect, telling them what to improve, deliberate practise includes specific, targeted advice from their teacher or coach on how to improve.

 

Suppose, for example, a pupil has recently been introduced to the idea of multiplication over a bracket and is well rehearsed at writing expressions such as 2(x+5) in their expanded form but is making the (very common) error of occasionally forgetting to multiply the second term and instead taking their cue from the operator, so they are writing solutions such as 2(x+5) = 2x+7 or 4(3x-6) = 12x-2 every now and then.  They have worked doggedly to reduce their error rate and now only make this slip every one in 100 times.  It is not the case that they don’t know what they are doing, but still these little errors are creeping in.

 

At the deliberate practise step, their teacher speaks to them about the errors they are making and, because we have been teaching mathematics for millennia and know a huge amount about how to overcome common misconceptions, the teacher then instructs the pupil in a method that is known to address this very specific issue (in this case, for example, when pupils are missing the need to multiply the second term, we can show the pupil an alternative format for presenting the problem, such as a grid or area, which really hammers home the need to multiply).  Now the pupil can advance further and improve their performance to elite standard.

 

Having elite performance in every little micro-skill of mathematics means that, when these skills inevitably appear in future areas of mathematics, the pupil is free to concentrate on the new idea and has no demand on their mental energy when dealing with the component micro-skills.  This is what I was referring to earlier when I described pupils having the mathematical grammar that allows them to have a meaningful discussion about a new idea.

 

(Side note: Deliberate practise is what is most often being described when people talk about ‘coaching’.  In schooling, it is the expert subject teacher who acts as the coach.  Coaching is only possible in domains where there exist agreed standards of excellence.  This is why it is a myth that we can coach people how to be a teacher – since teaching, and education as a whole, is a domain with no shared standards of excellence, which I find deeply saddening and hope that, one day, the ideological bickering will end, and we can iterate together towards such a set of standards.)

 

Bringing about connectivity

 

As mentioned earlier, the stages I am describing are not linear.  Connectivity could and should be a focus throughout.  I place it here in the story simply because it is when pupils have achieved a level of fluency that connectivity becomes truly exciting and joyful.

 

Mathematics, in common with most subjects, is not a dull march through a tick-list of marketable skills that happen to stack up in a precise order.  Mathematics is far better conceptualised as interconnected webs of ideas. The individual ideas and the webs they form interact with all others.  As the pupil learns more and more ideas, they are able to see the bigger picture or the stories the webs tell and the more and more of these webs that are weaved, the more vantage points they have to look at old ideas afresh and build new mathematical understanding.

 

Teachers can help pave the way to connectivity by ensuring the methods and approaches they introduce pupils to are ‘forward-facing’, which is to say that they continue to hold true as the subject evolves and new ideas build on old.  Taking a forward-facing approach helps to weave into existence a narrative that links prior learning to current learning to future learning.  It helps to demystify mathematics and make it easier for pupils to grip new ideas without the unnecessary step of undoing previously held misconceptions.

 

Additionally, taking a forward-facing approach to teaching mathematics significantly increases the moments of wonder and joy that pupils will experience throughout their time at school and beyond – those beautiful moments when a light goes on above a pupil’s head and they exclaim, ‘ah, so that’s why we learnt that thing years ago!’  Imagine, for example, the pupil who has experienced a forward-facing education being able to follow the thread from learning about casting shadows in pre-school, through reflections and rotations in primary, vectors and matrices in secondary and culminating with the revelation of eigenvectors and values and all their wondrous uses as they pull it all together during a mathematics degree and realise their mathematics education was a continuum and a story.

 

Connectivity in learning mathematics unlocks the power of transfer; when pupils are able to draw on ideas they have learnt about in the past and use them like tools in their mathematical repertoire to attack unfamiliar problems in entirely different circumstances to when they first encountered the ideas, combining many different ideas in applications of mathematics so varied and interesting that they are able to begin to behave as mathematicians behave, knowing when and why to select particular methods and how to adapt them to meet new demands.

 

Bringing about maturation

 

Time.  Really, it’s about time.

 

As pupils learn mathematics, over many years, webs of ideas form and the connections between them strengthen.  Pupils can shine entirely new light on old ideas and can see how mathematics is not static.

 

This final step in becoming expert is all about pupils having ample opportunity to behave mathematically in genuine and sincere ways, working on meaningful problems and properly having the chance to see mathematics as a way of thinking, a way of being.

 

It is through these opportunities that pupils are able see mathematics as a living and breathing subject, one with a history and a future, one where every single idea that it contains is merely a point on a journey.  Mathematics is a great truth making machine, it iterates and improves.  The subject is a battleground.

 

Every idea that is currently accepted in mathematics marks the point at which one idea was defeated by a new, more powerful idea.  Mathematics has a history, it is moving and continuous, which means schools seeking to give pupils the mechanisms for bringing about the best which will be thought and said in the future, must present mathematics as histories.

 

To become educated means to become aware of the origins and growth of knowledge and knowledge systems; to be familiar with the intellectual and creative processes by which the best which has been thought and said has been produced; to learn how to participate in what Robert Maynard Hutchins once called ‘The Great Conversation’.

 

Behaving mathematically is the main focus of my next book, so I will leave further discussion of maturation until then.

 

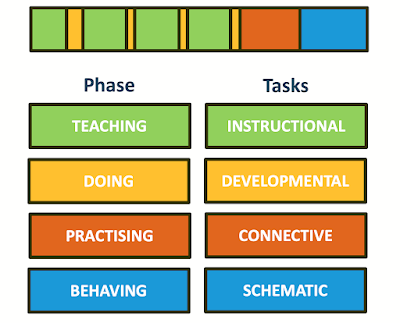
Phases of learning

 

Some readers might recognise the discussion above as an alternative articulation of my ‘Teach, Do, Practise, Behave’ model of learning (see my 2019 Teaching for Mastery book).  

 

 

As the TDPB model evolves in my head, I am keen to describe its structure further.  The brief descriptions of the stages above are hopefully a quick insight into that structure.  In the next part of this blog, I will take each of the stages and describe them more fully, with a particular emphasis on how this might practically be applied in the classroom in a coherent approach to teaching and learning.

 

A coherent approach to teaching and learning can significantly increase the chances of every single pupil successfully gripping mathematics, but we have allowed actors in the education space to promulgate the notion that we do not know the most effective ways of teaching and that learning is some mystical, unknowable quiddity.  This narrative is used to justify continual experimentation and fads.  There is perhaps no more damaging an idea in education than the idea that we have no idea about education.  We know lots about how to educate and what it means to be an educated person.  We should not shy away from that knowledge, which has been so hard won by generations of educators before us.  Let’s not deny any pupil the benefits of that knowledge.